Transportation Problem
The transportation problem is a special type of linear programming problem where the objective consists in minimizing transportation cost of a given commodity from a number of sources or origins (e.g. factory, manufacturing facility) to a number of destinations (e.g. warehouse, store). Each source has a limited supply (i.e. maximum number of products that can be sent from it) while each destination has a demand to be satisfied (i.e. minimum number of products that need to be shipped to it). The cost of shipping from a source to a destination is directly proportional to the number of units shipped.
Basic Notation:
- m = number of sources (i = 1 … m)
- n = number of destinations (j = 1 … n)
- c i,j = unit cost of shipping from source i to destination j
- x i,j = amount shipped from source i to destination j
- a i = supply at source i
- b j = demand at destination j
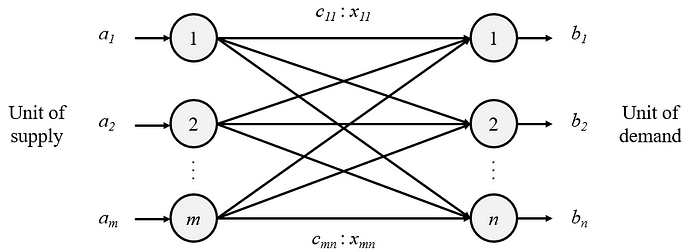
Sources are represented by rows while destinations are represented by columns. In general, a transportation problem has m rows and n columns. The problem is solvable if there are exactly (m+n-1) basic variables.

Comments
Post a Comment